Car Trajectory Optimization with PSO

Here is my TIPE project for the 2023/2024 academic year, based on the theme "Sports and Games".

You can find the code for this project on my GitHub.

Introduction

I am a big fan of motorsports, which is why I decided to optimize a car's trajectory on a track. To do this, I used a Swarm Optimization (PSO) algorithm, a metaheuristic inspired by bird flocking behavior.

Shortly after, I realized that the algorithm relies on many parameters that were not detailed in the articles. I therefore had to conduct extensive research to find the best parameters for my problem, which became the focus of my TIPE.

The algorithm parameters I will estimate are:

  • The number of particles
  • The number of iterations
  • The inertia weight w
  • The cognitive coefficients c1
  • The social coefficients c2

I will use the French Grand Prix track, named Paul Ricard:

Circuit Paul Ricard

The articles provide the formula for updating particle velocities, which is:

v(t+1) = w·v(t) + c₁·r₁·(pbest - x(t)) + c₂·r₂·(gbest - x(t))

Where w, c₁ and c₂ are the parameters we want to estimate.

The inertia weight parameter

The first parameter we will estimate is w. To do this, I will fix the other parameters and vary w.

Here are the results:

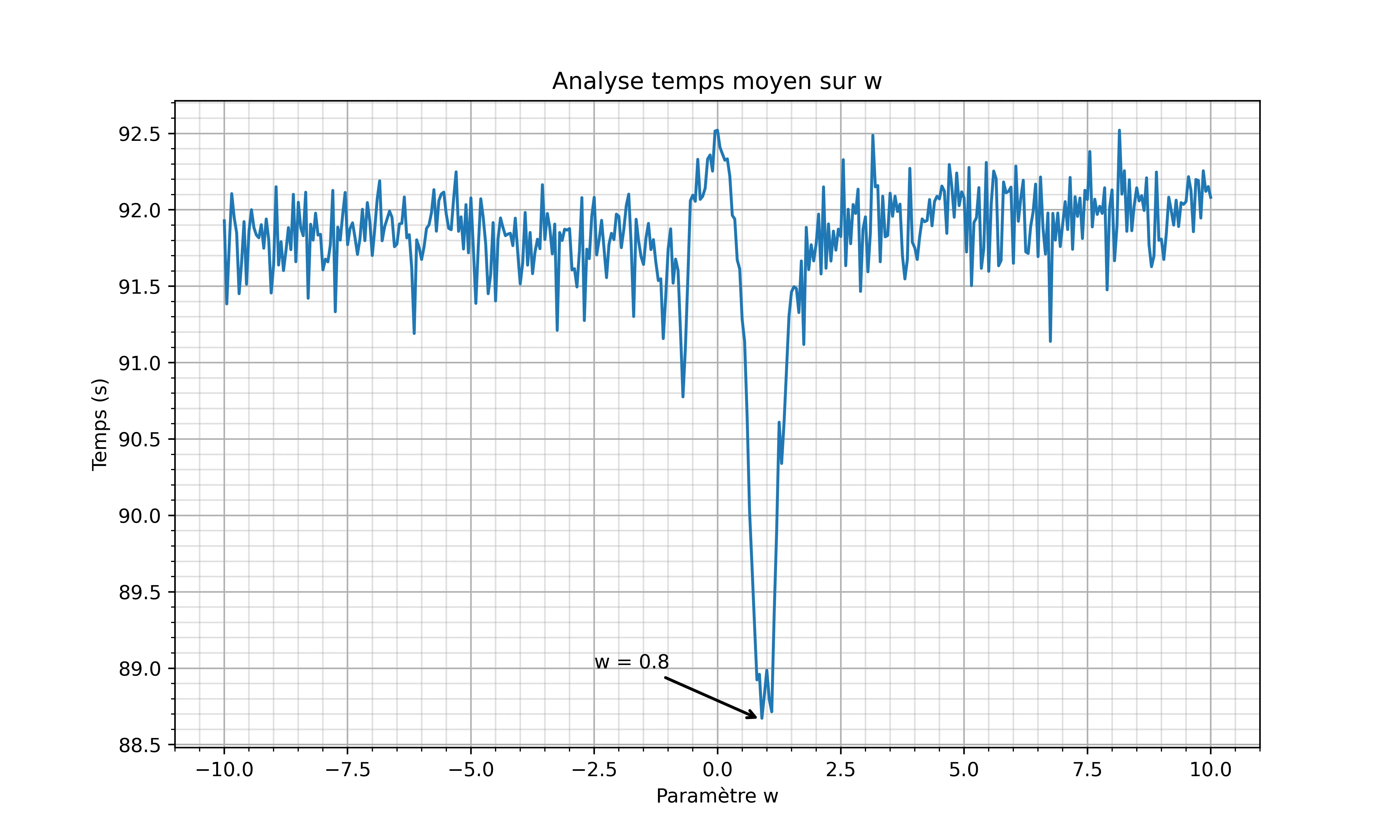
Analyse du poids w

We can see that the best value for w is 0.8.

The number of iterations and particles

The second and third parameters we will estimate are the number of iterations and particles. Since these are nested loop variables, they will have the same effect on computation time. We will therefore study their effect on lap time.

Here are the results:

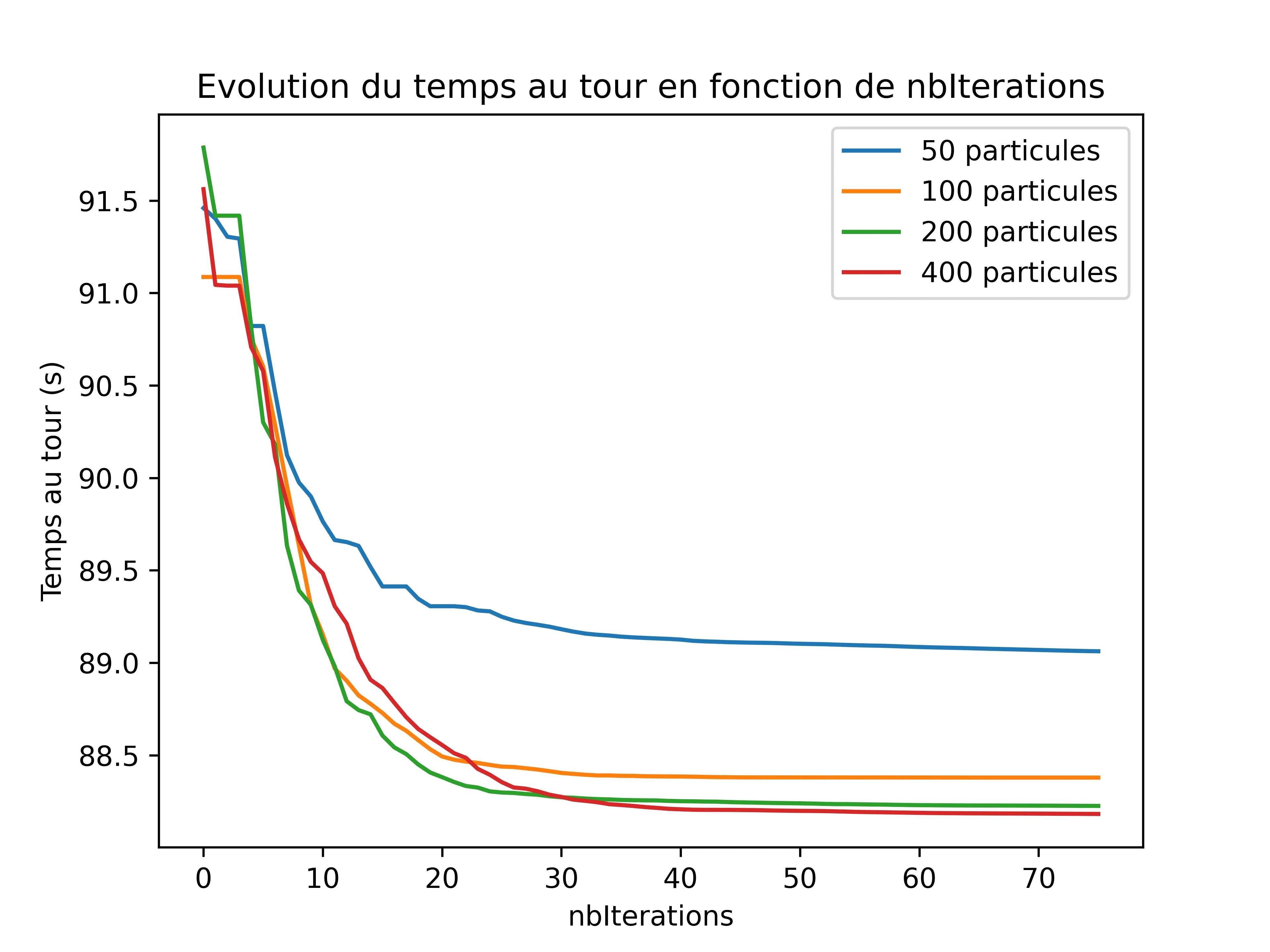
Analyse itérations vs particules

We can clearly see that after 50 iterations, the lap time stabilizes. As for the number of particles, we can see that it tends to reach a limit. This means that if you want better results, you can use a larger number of particles, but if you want faster results, you can opt for a smaller number of particles.

The social and cognitive coefficients (gbest and pbest)

The last parameters we will estimate are the social and cognitive coefficients. To do this, we will search for a minimum on a plane using the simulated annealing algorithm. I ran this on a computing farm with 64 processes each time.

Here are the results:

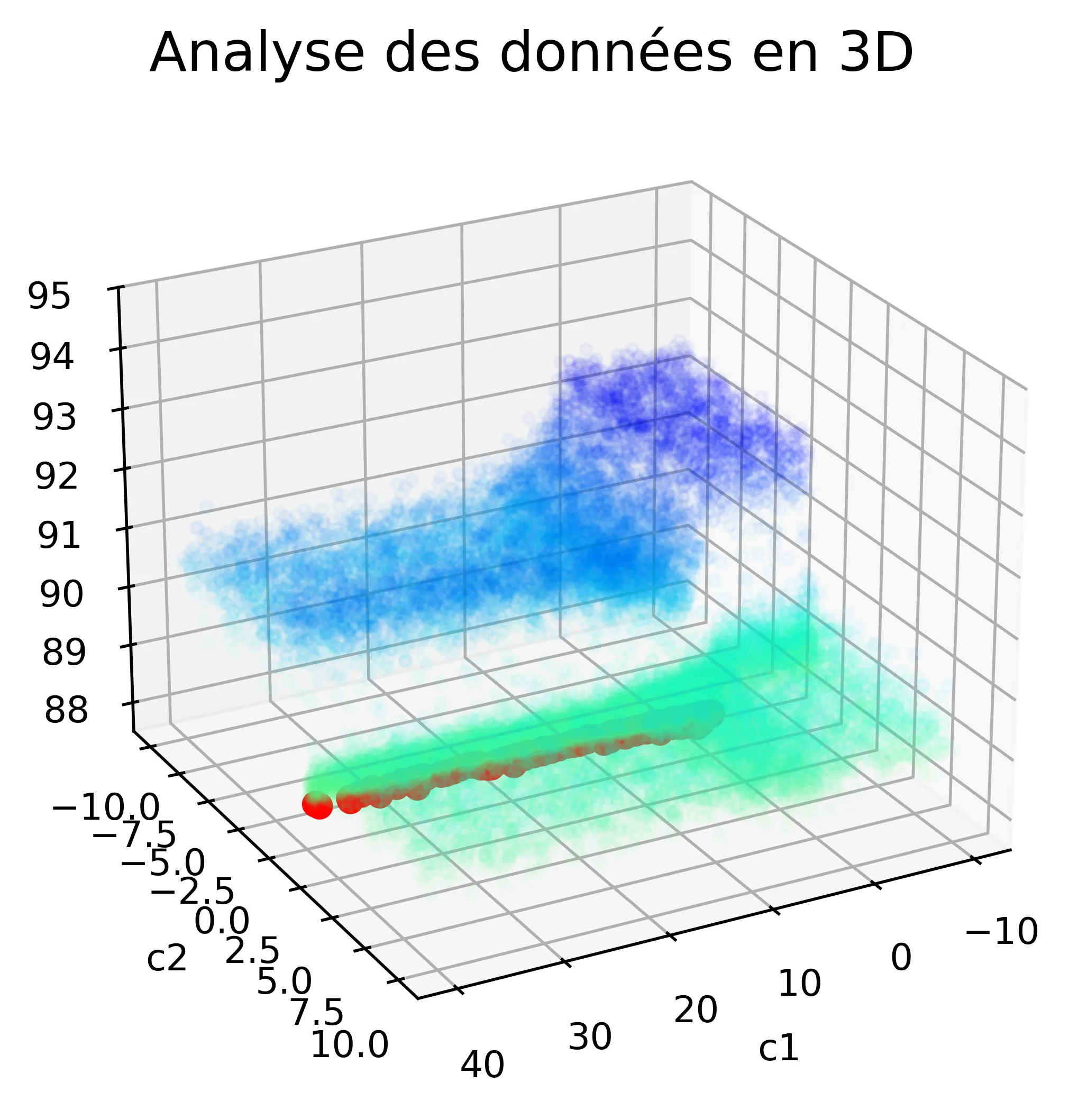
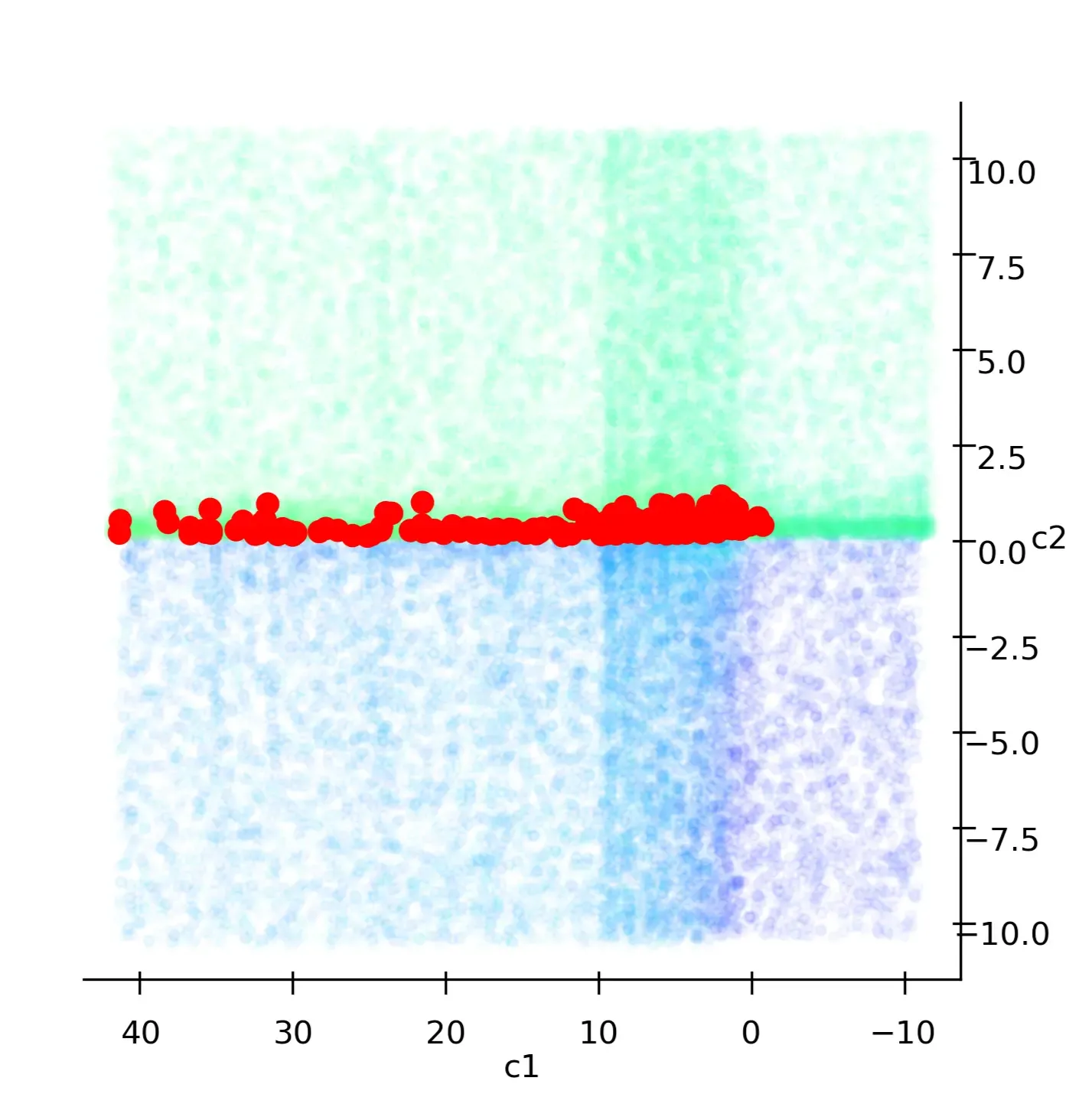
Analyse 3D de c1 et c2 Vue 2D de c1 et c2

We can see that c₁ values must be strictly positive.

As for c₂, I will analyze the distribution of its values.

Here are the results:

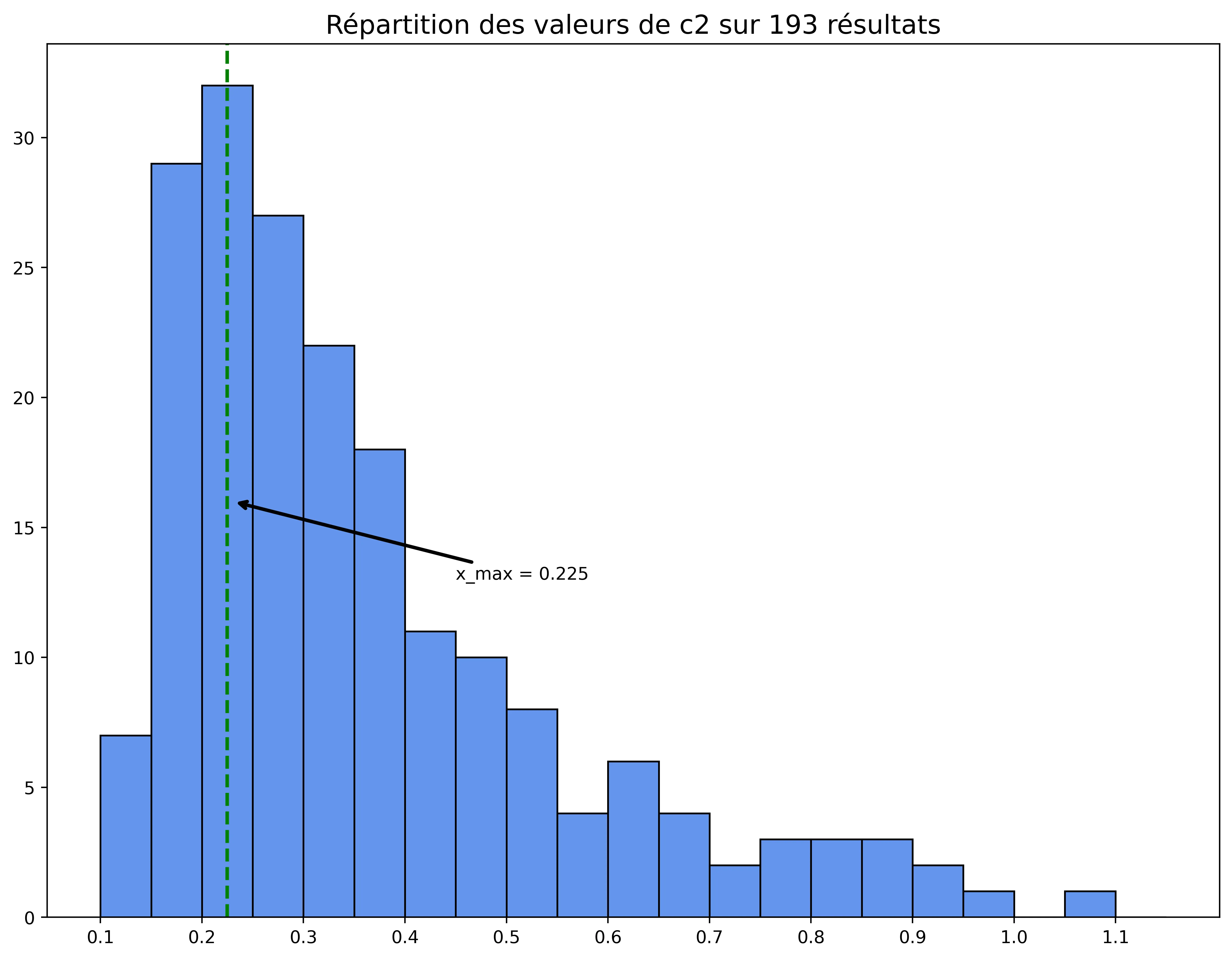
Analyse de c2

We can see that the best value for c₂ is 0.225.

The final analysis result

After all these analyses, we determined that the best parameters for the PSO algorithm are:

  • Number of particles: 80-400+ (can be chosen based on desired computation time or result accuracy)
  • Number of iterations: 50
  • Inertia weight w: 0.8
  • Cognitive coefficient c₁: > 0
  • Social coefficient c₂: 0.225

The racing line

After all these analyses, we found the optimal parameters for the PSO algorithm. We can now proceed to calculate racing lines.

Here is one of the computed racing lines:

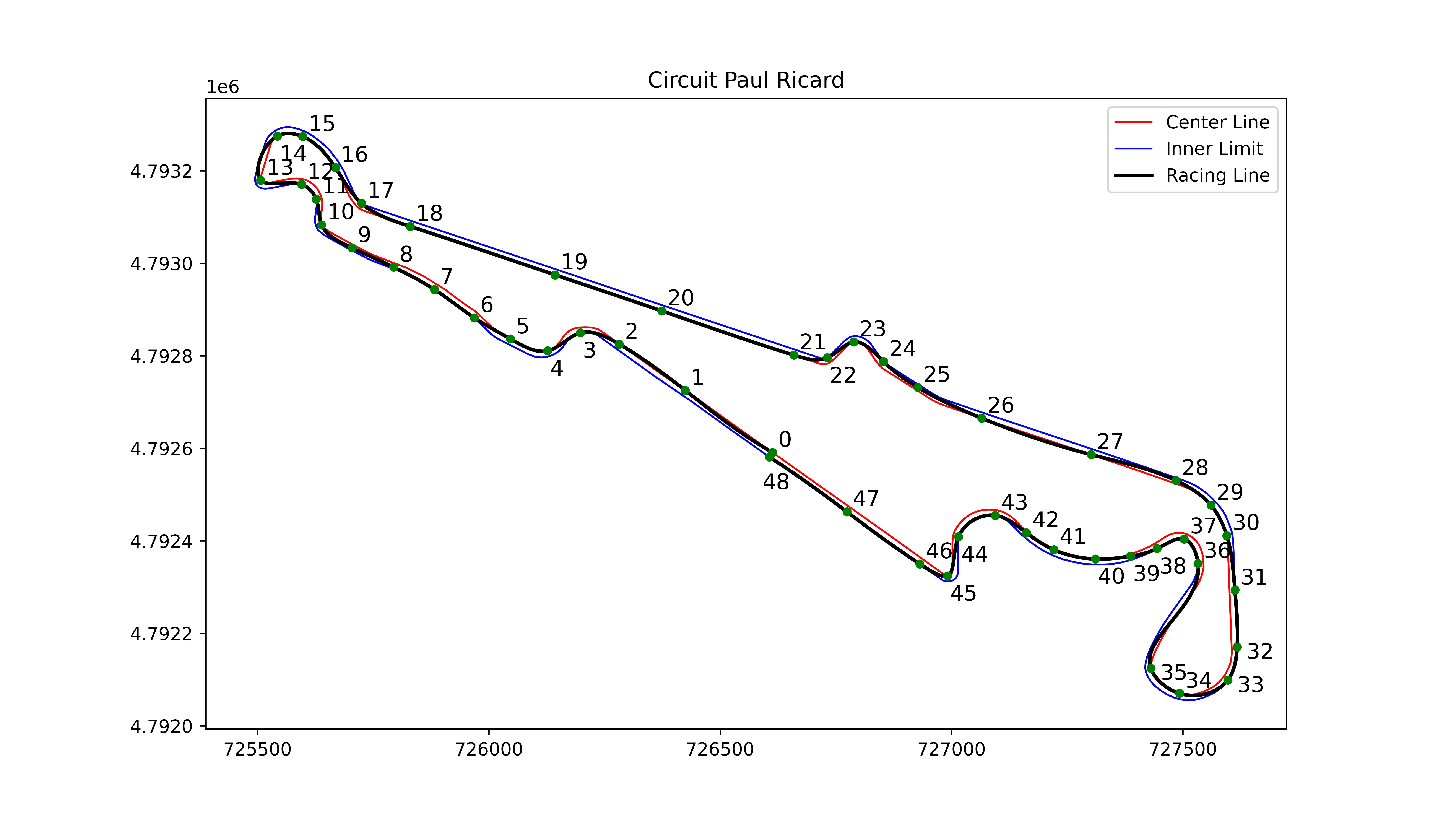
Trajectoire de course optimale

This concludes my TIPE project. I hope you enjoyed reading it as much as I enjoyed working on it.

If you have any questions or would like to know more about my project, feel free to contact me by email or via social media.

References

  • YING XIONG : Racing Line Optimization : Massachusetts Institute of Technology (2010)
  • H. BUTLER, M. DALY, A. DOYLE, S. GILLIES, S. HAGEN, T. SCHAUB : The GeoJSON Format
  • INTERNATIONAL CIVIL AVIATION ORGANIZATION : World Geodetic System 1984 (WGS-84) Manual
  • J. KENNEDY, R.C. EBERHART : Particle swarm optimization : Proceedings of ICNN'95 - International Conference on Neural Networks, pp. 1942-1948 vol.4, (1995), Perth, Australia, doi: 10.1109/ICNN.1995.4889
  • A. NICKABADI, M. MEHDI EBADZADEH, R. SAFABAKHSH : A novel particle swarm optimization algorithm with adaptive inertia weight : Applied Soft Computing, Volume 11, Issue 4, 2011, Pages 3658-3670, ISSN 1568-4946
  • A.C. BANSAL, P.K. SINGH, N.R. PA : Evolutionary and Swarm Intelligence Algorithms : Springer-Nature, 2018, ISBN: 978-3-319-91341-4
  • A. GRAY, E. ABBENA ,S. SALAMON : Modern Differential Geometry of Curves and Surfaces with Mathematica Third Edition : Chapman & Hall/CRC, 2006, ISBN: 1584884487