Optimisation de la trajectoire d'une voiture avec PSO

Voici mon projet de TIPE pour l'année académique 2023/2024, basé sur le thème "Sport et Jeux".

Vous pouvez trouver le code de ce projet sur mon GitHub.

Introduction

Je suis un grand amateur de sport automobile, c'est pourquoi j'ai décidé d'optimiser la trajectoire d'une voiture sur une piste. Pour ce faire, j'ai utilisé un algorithme de Swarm Optimization (PSO), une métaheuristique inspirée du comportement des volées d'oiseaux.

Peu de temps après, j'ai réalisé que l'algorithme repose sur de nombreux paramètres qui n'étaient pas détaillés dans les articles. J'ai donc dû mener des recherches approfondies pour trouver les meilleurs paramètres pour mon problème, qui sont devenus le centre de mon TIPE.

Les paramètres de l'algorithme que je vais estimer sont :

  • Le nombre de particules
  • Le nombre d'itérations
  • Le poids d'inertie w
  • Les coefficients cognitifs c1
  • Les coefficients sociaux c2

Je vais utiliser la piste du Grand Prix de France, nommée Paul Ricard :

Circuit Paul Ricard

Les articles fournissent la formule pour mettre à jour la vitesse des particules, qui est :

v(t+1) = w·v(t) + c₁·r₁·(pbest - x(t)) + c₂·r₂·(gbest - x(t))

Où w, c₁ et c₂ sont les paramètres que nous voulons estimer.

Le paramètre de poids d'inertie

Le premier paramètre que nous allons estimer est w. Pour ce faire, je vais fixer les autres paramètres et faire varier w.

Voici les résultats :

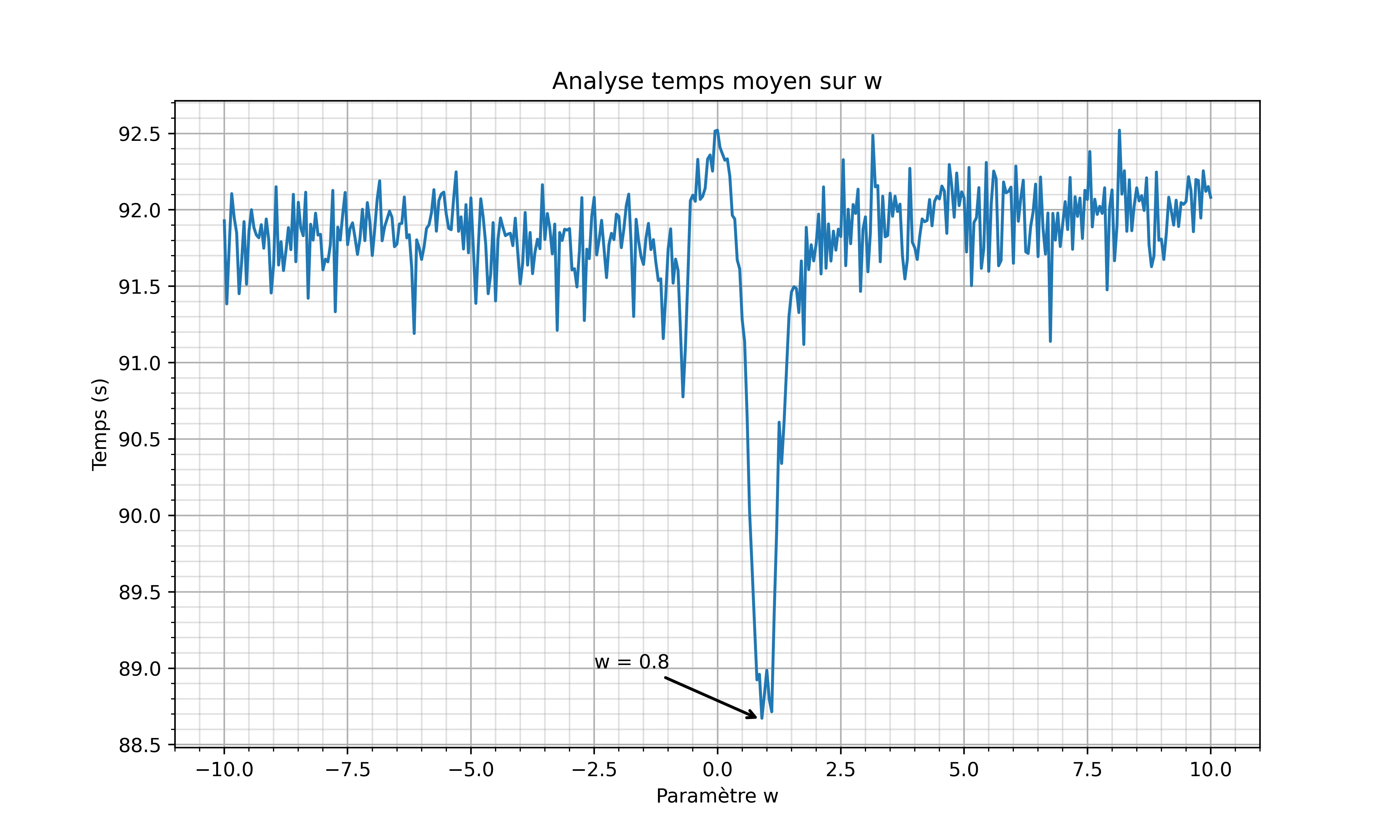
Analyse du poids w

Nous pouvons voir que la meilleure valeur pour w est 0.8.

Le nombre d'itérations et de particules

Les deuxième et troisième paramètres que nous allons estimer sont le nombre d'itérations et de particules. Comme ce sont des variables de boucles imbriquées, ils auront le même effet sur le temps de calcul. Nous allons donc étudier leur effet sur le temps au tour.

Voici les résultats :

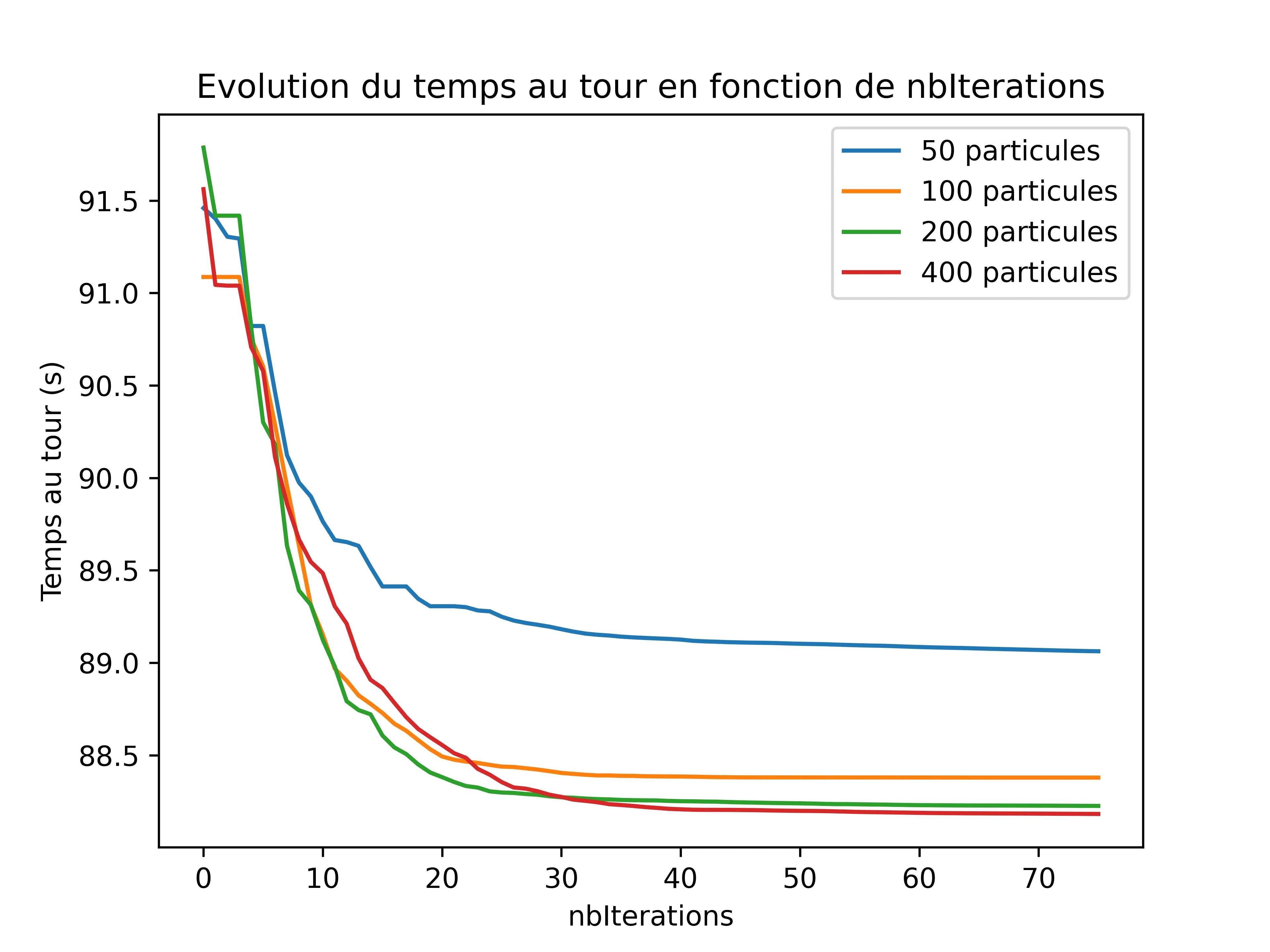
Analyse itérations vs particules

Nous pouvons clairement voir qu'après 50 itérations, le temps au tour se stabilise. Quant au nombre de particules, nous pouvons voir qu'il tend à atteindre une limite. Cela signifie que si vous voulez de meilleurs résultats, vous pouvez utiliser un plus grand nombre de particules, mais si vous voulez des résultats plus rapides, vous pouvez opter pour un nombre plus faible de particules.

Les coefficients sociaux et cognitifs (gbest et pbest)

Les derniers paramètres que nous allons estimer sont les coefficients sociaux et cognitifs. Pour ce faire, nous allons chercher un minimum sur un plan avec l'algorithme du recuit simulé. J'ai exécuté cela sur une ferme de calcul sur 64 processus à chaque fois.

Voici les résultats :

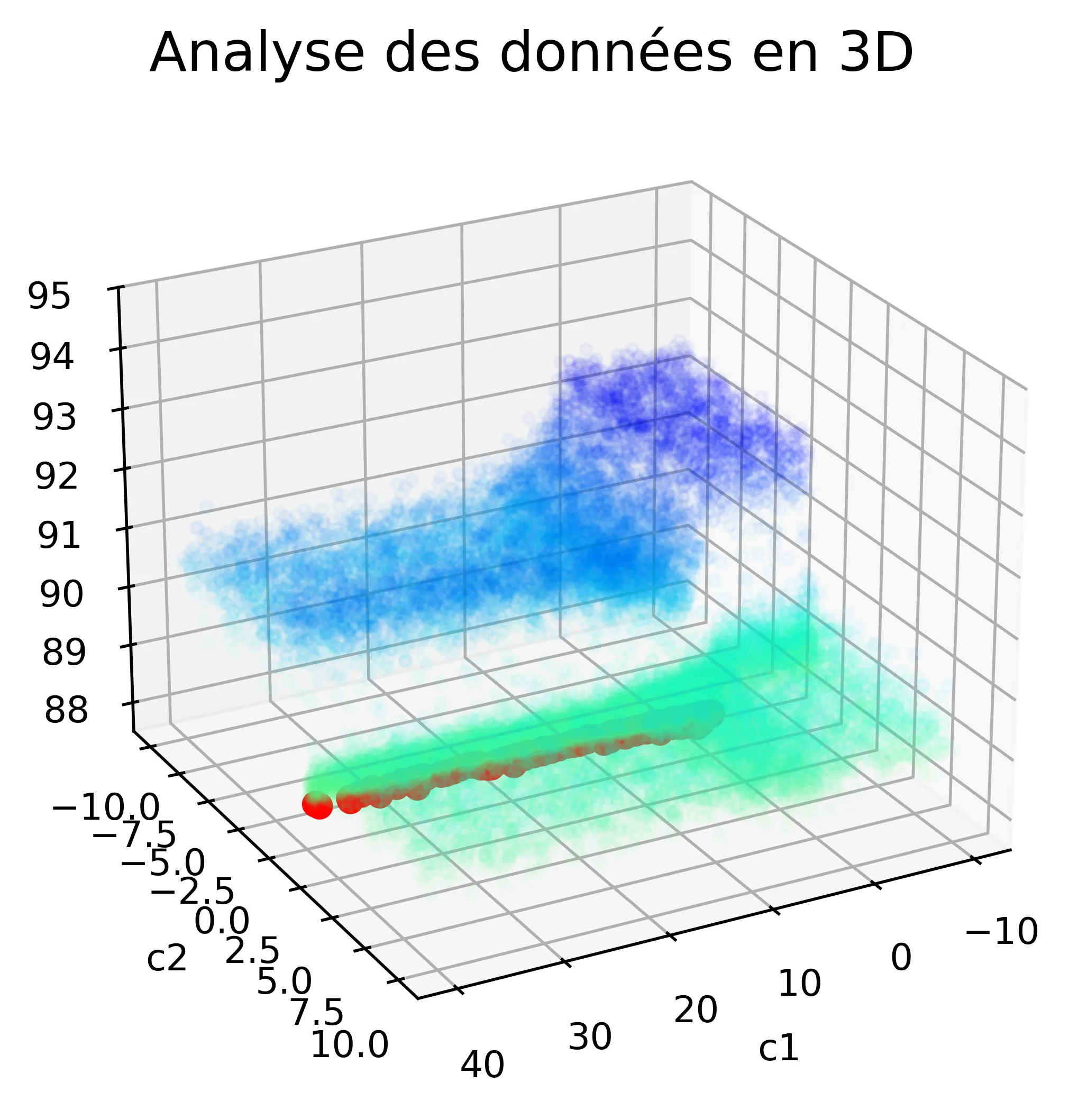
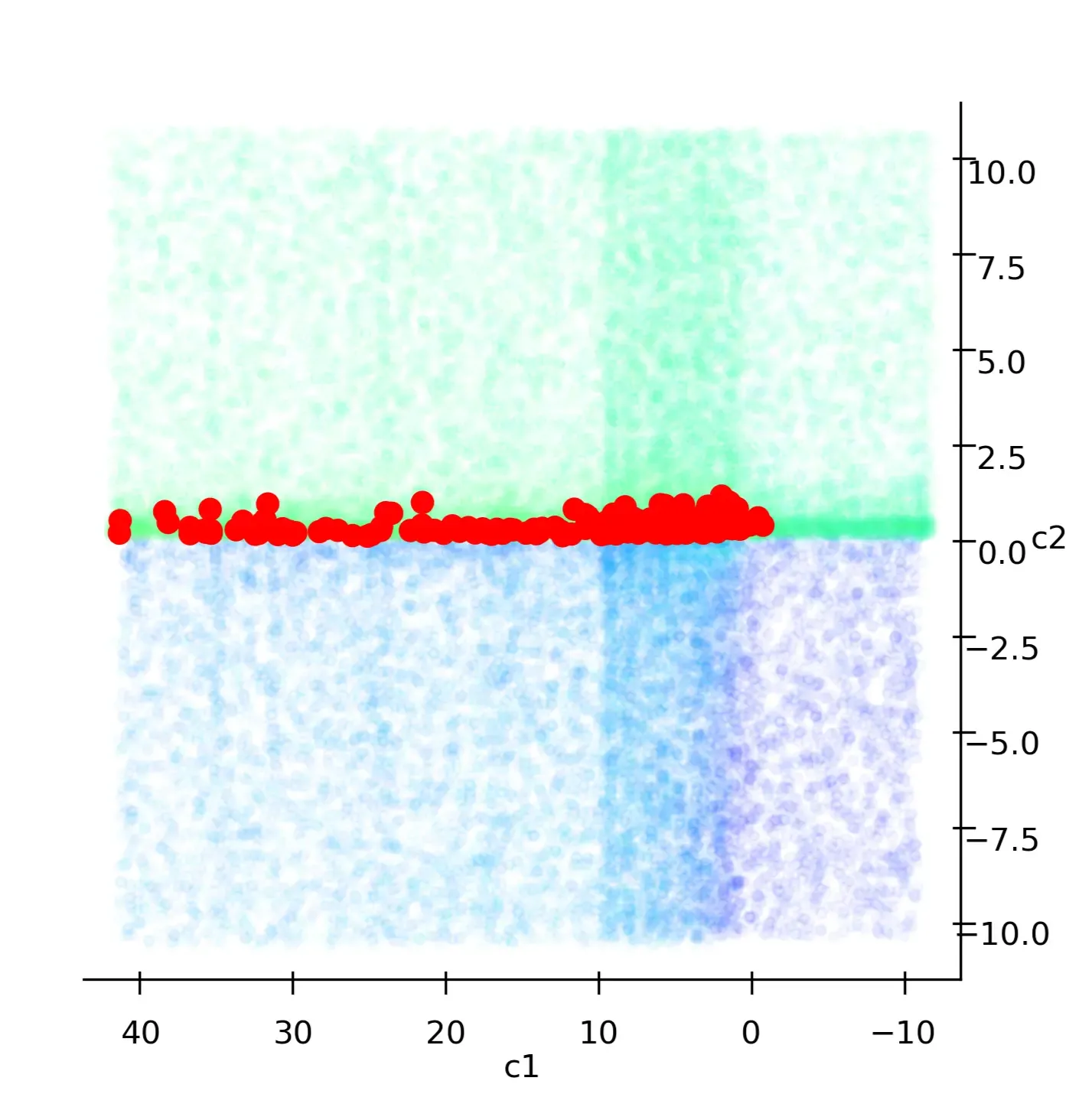
Analyse 3D de c1 et c2 Vue 2D de c1 et c2

Nous pouvons voir que les valeurs de c₁ doivent être strictement positives.

Quant à c₂, je vais analyser la distribution de ses valeurs.

Voici les résultats :

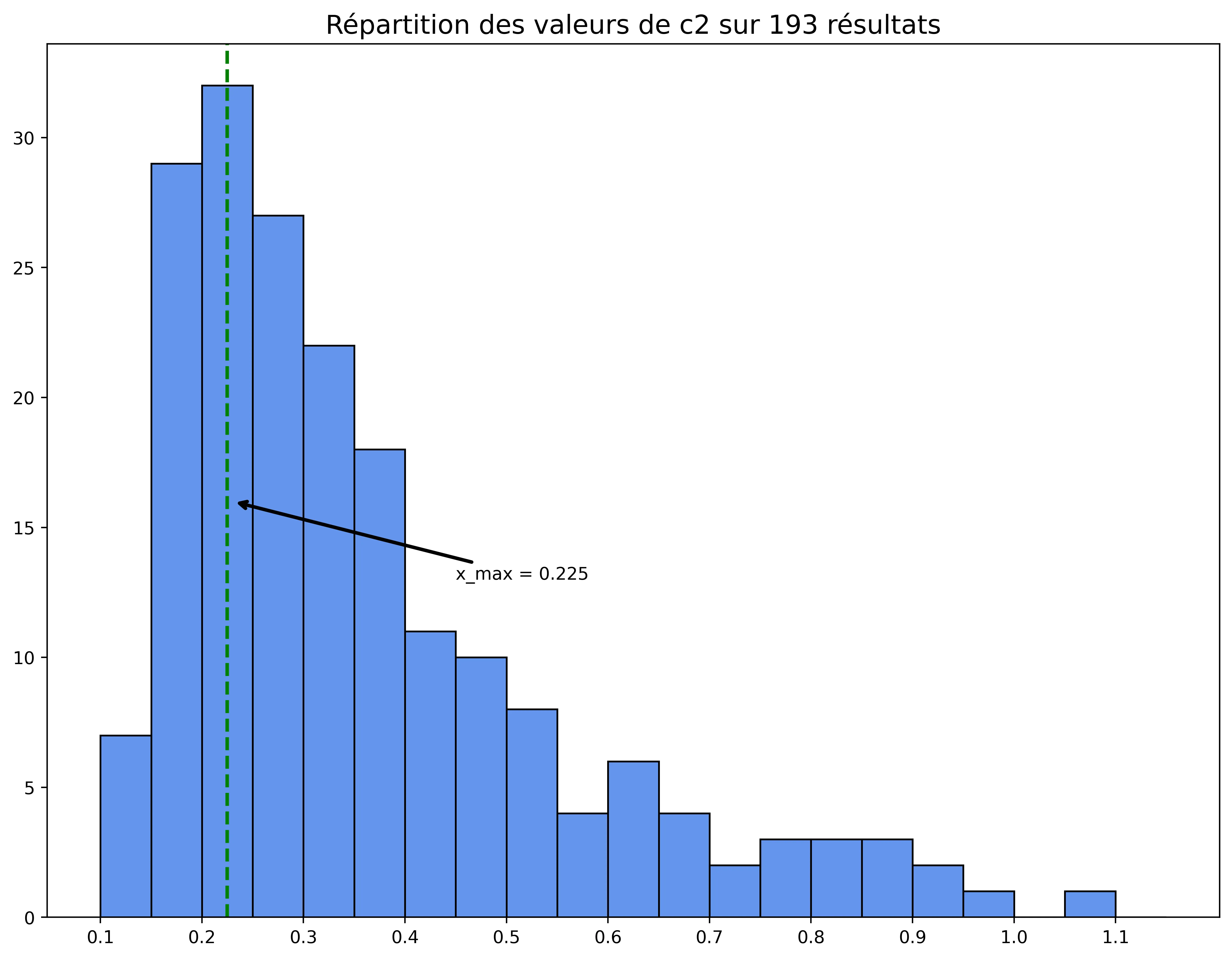
Analyse de c2

Nous pouvons voir que la meilleure valeur pour c₂ est 0.225.

Le résultat final de l'analyse

Après toutes ces analyses, nous avons déterminé que les meilleurs paramètres pour l'algorithme PSO sont :

  • Nombre de particules : 80-400+ (peut être choisi en fonction du temps de calcul souhaité ou de la précision des résultats)
  • Nombre d'itérations : 50
  • Poids d'inertie w : 0.8
  • Coefficient cognitif c₁ : > 0
  • Coefficient social c₂ : 0.225

La trajectoire de course

Après toutes ces analyses, nous avons trouvé les paramètres optimaux pour l'algorithme PSO. Nous pouvons maintenant procéder au calcul des trajectoires de course.

Voici l'une des trajectoires de course calculées :

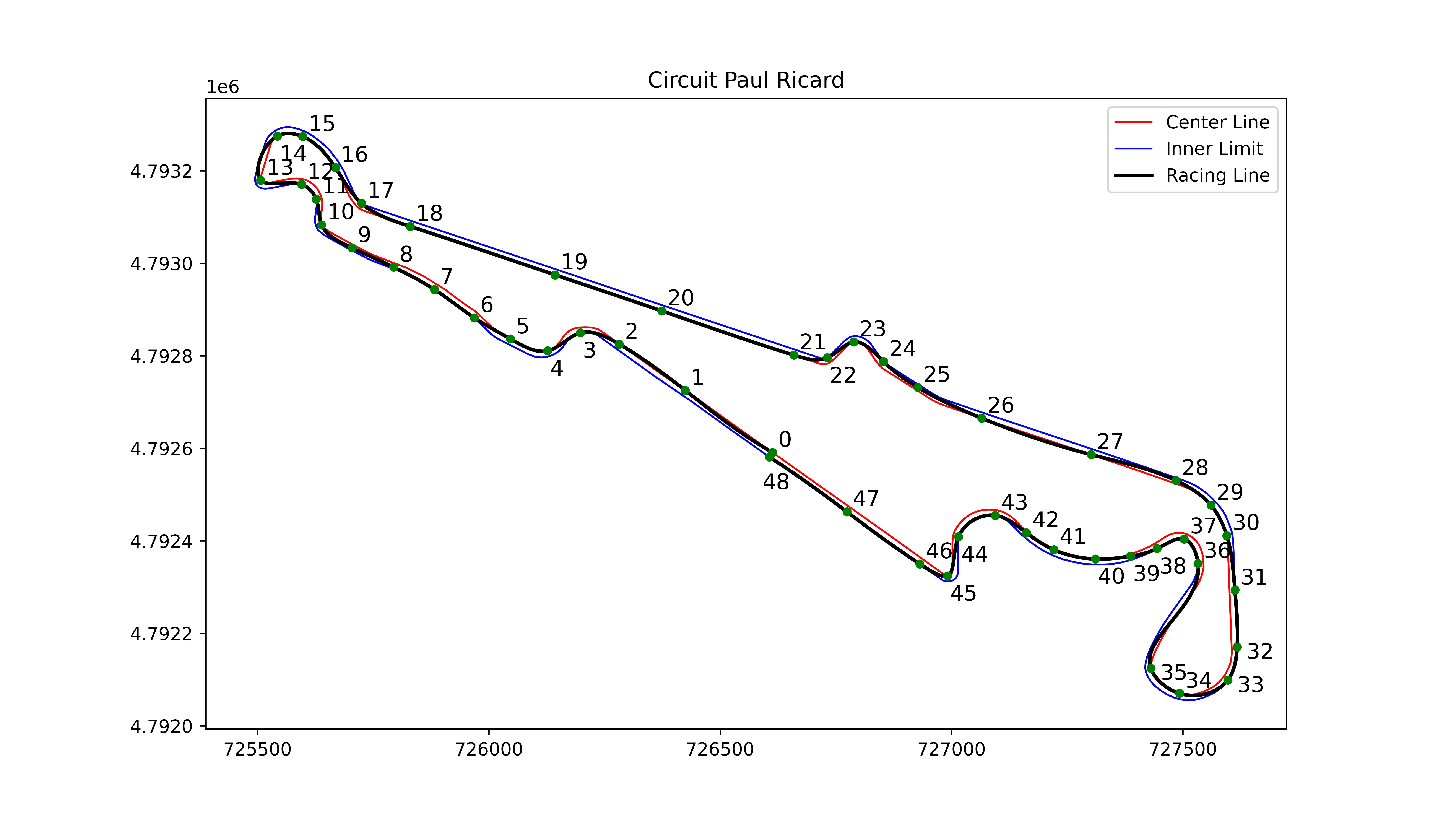
Trajectoire de course optimale

Cela conclut mon projet de TIPE. J'espère que vous avez apprécié le lire autant que j'ai apprécié le travailler.

Si vous avez des questions ou si vous souhaitez en savoir plus sur mon projet, n'hésitez pas à me contacter par email ou via les réseaux sociaux.

Références

  • YING XIONG : Racing Line Optimization : Massachusetts Institute of Technology (2010)
  • H. BUTLER, M. DALY, A. DOYLE, S. GILLIES, S. HAGEN, T. SCHAUB : The GeoJSON Format
  • INTERNATIONAL CIVIL AVIATION ORGANIZATION : World Geodetic System 1984 (WGS-84) Manual
  • J. KENNEDY, R.C. EBERHART : Particle swarm optimization : Proceedings of ICNN'95 - International Conference on Neural Networks, pp. 1942-1948 vol.4, (1995), Perth, Australia, doi: 10.1109/ICNN.1995.4889
  • A. NICKABADI, M. MEHDI EBADZADEH, R. SAFABAKHSH : A novel particle swarm optimization algorithm with adaptive inertia weight : Applied Soft Computing, Volume 11, Issue 4, 2011, Pages 3658-3670, ISSN 1568-4946
  • A.C. BANSAL, P.K. SINGH, N.R. PA : Evolutionary and Swarm Intelligence Algorithms : Springer-Nature, 2018, ISBN: 978-3-319-91341-4
  • A. GRAY, E. ABBENA ,S. SALAMON : Modern Differential Geometry of Curves and Surfaces with Mathematica Third Edition : Chapman & Hall/CRC, 2006, ISBN: 1584884487